Moment of Inertia of a Rectangle – Formula Derivation

Moment of Inertia of a Rectangle

The moment of inertia is one of the key properties of a body that determines its resistance to rotation. In planar geometry, it describes how the area is distributed relative to a specific axis. For a rectangle — one of the simplest and most commonly used shapes — the moment of inertia can be derived analytically, although it is based on a fundamental integral definition.

What is Moment of Inertia?

For a planar shape, the moment of inertia with respect to an axis (e.g., x or y) is defined as a second-order area integral:

Where:

A — area of the shape
x, y — coordinates within the area
Ix — moment of inertia about the x-axis
Iy — moment of inertia about the y-axis

Rectangle: Problem Setup

Consider a rectangle of width b and height h, centered at the origin (0,0), with sides aligned to the axes. The integration limits are: x from −b⁄2 to b⁄2, and y from −h⁄2 to h⁄2.

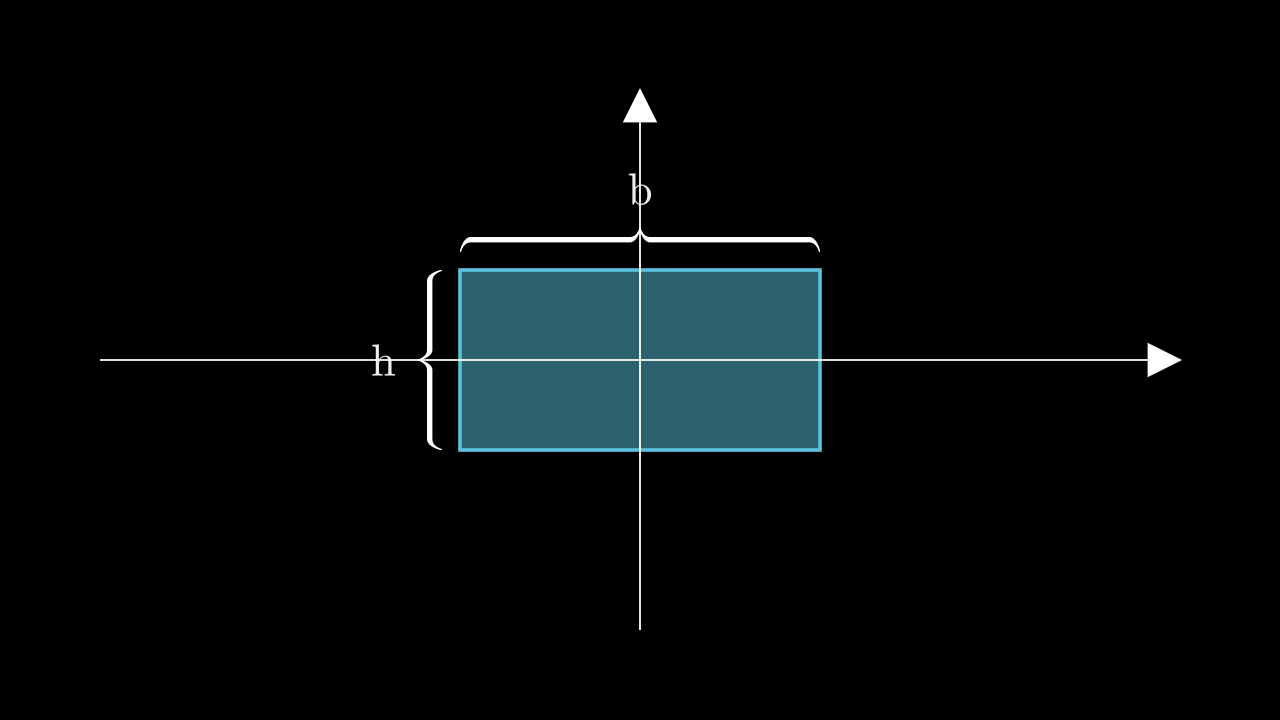
Derivation of Ix (about the x-axis)

Img error Ix = S(-b/2)(b/2) S(-h/2)(h/2) y^2 dydx

First, integrate with respect to y:

Then integrate with respect to x:

Final formula:

Derivation of Iy (about the y-axis)

First, integrate with respect to y:

Then integrate with respect to x:

Final formula:

Geometric Meaning

These formulas show that Ix depends more on the height h (raised to the 3rd power), and Iy depends on the width b. This matches intuition: the farther mass (or area) is distributed from an axis, the harder it is to rotate the object around that axis. Thus, a tall and narrow shape will have a high moment of inertia about the horizontal axis and a low one about the vertical.

Practical Applications

Moments of inertia are crucial in:

Mechanics (torsion and bending calculations)
Structural engineering (beams, trusses, bridges)
Visualization and physical simulation (object behavior modeling)

For arbitrary shapes, the moment of inertia is usually computed numerically — e.g., using triangulation and summing over triangles (as in CAD or FEM software). But for simple shapes like rectangles, analytical formulas offer quick and accurate results.