Моменты инерции прямоугольника. Вывод формулы.

Моменты инерции прямоугольника

Момент инерции — одна из ключевых характеристик тел, определяющая их инерционные свойства при вращении. В контексте плоской геометрии он отражает распределение площади фигуры относительно некоторой оси. Для прямоугольника, одной из самых простых и часто используемых форм, момент инерции легко поддаётся аналитическому выводу, но за ним стоит фундаментальное интегральное определение.

Что такое момент инерции?

Для плоской фигуры момент инерции относительно оси (например, оси x или y) определяется как интеграл второго порядка:

Здесь:

A — площадь фигуры
x,y — координаты точки в пределах этой области
Ix — момент инерции относительно оси x
Iy — момент инерции относительно оси y

Прямоугольник: постановка задачи

Рассмотрим прямоугольник шириной b и высотой h, расположенный симметрично относительно начала координат: его центр находится в точке (0,0), а стороны параллельны осям. Пределы интегрирования тогда будут: по x: от −2b до b2, по y: от −h2 до h2.

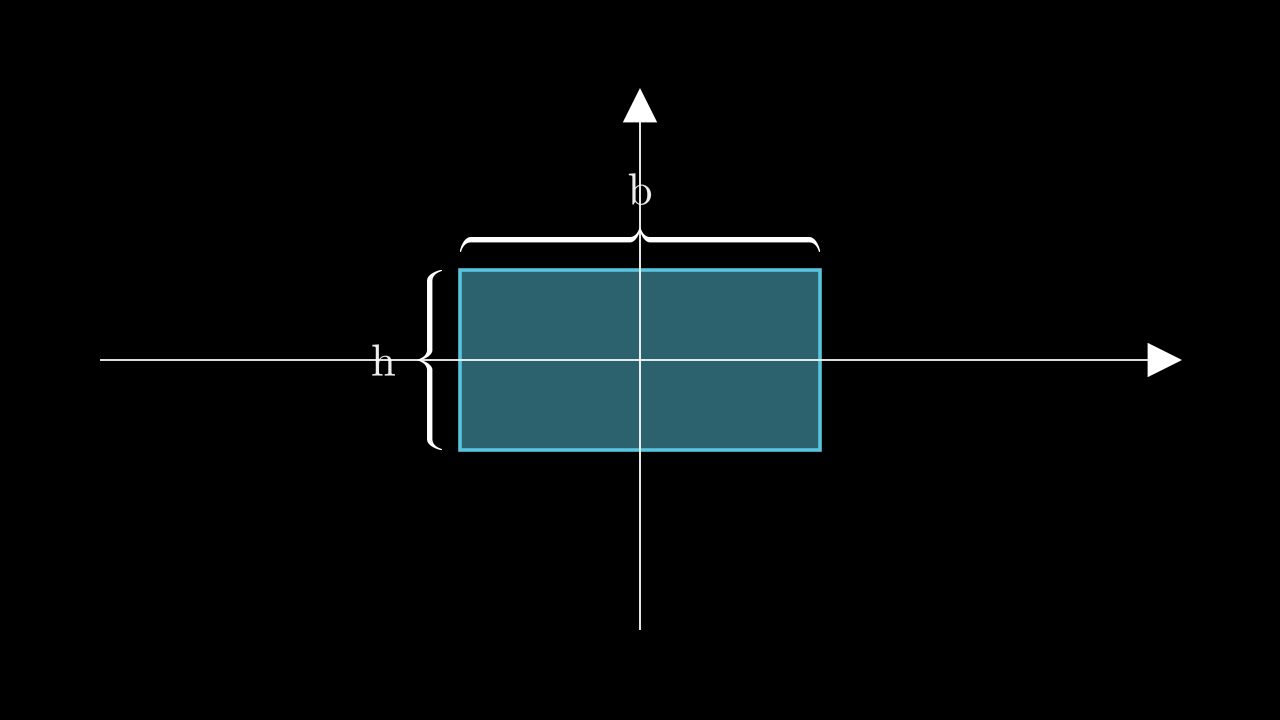
Вывод момента инерции относительно оси x

Img error Ix = S(-b/2)(b/2) S(-h/2)(h/2) y^2 dydx

Выполняем интегрирование по y:

Выполняем интегрирование по x:

Окончательная формула:

Вывод момента инерции относительно оси y

Выполняем интегрирование по y:

Выполняем интегрирование по x:

Окончательная формула:

Геометрический смысл

Эти формулы демонстрируют, что: Ix сильнее зависит от высоты h, так как она в кубе, Iy — от ширины bb. Это отражает интуитивное понимание: чем дальше масса (или площадь) удалена от оси, тем труднее «раскрутить» фигуру относительно этой оси. Поэтому высокая и узкая фигура будет иметь большой момент инерции относительно горизонтальной оси и маленький — относительно вертикальной.

Практическое значение

Моменты инерции играют важную роль:

в механике (расчёт сопротивления при кручении и изгибе)
в инженерии конструкций (балки, фермы, мосты)
в визуализации и физическом моделировании (симуляция поведения объектов)

Для произвольных фигур момент инерции вычисляется численно — например, с помощью триангуляции фигуры и суммирования по треугольникам (как делается в CAD или FEM-софте). Но для простых форм, как прямоугольник, аналитические формулы обеспечивают быстрые и точные оценки.